PyTorchで高速フーリエ変換(離散フーリエ変換)をするには、torch.fft.fftを使う。torch.fft.fftの使い方と、正弦波に対してFFTを行い、周波数特性を確認する。
torch.fft.fftの使い方
torch.fft.fftの第一引数inputにTensor配列を指定しれば、高速フーリエ変換の結果が返ってくる。
import torch
t = torch.arange(10)
print(t)
# tensor([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])
T = torch.fft.fft(input=t)
print(T)
# tensor([45.+0.0000j, -5.+15.3884j, -5.+6.8819j, -5.+3.6327j, -5.+1.6246j,
# -5.+0.0000j, -5.-1.6246j, -5.-3.6327j, -5.-6.8819j, -5.-15.3884j])第二引数nを指定すると、その長さの信号長でFFTされる。n=3を指定すれば、3サンプルまでの信号でFFTされ、逆にn=20など信号長より長くすると、その分0埋めされた信号でFFTされる。
T = torch.fft.fft(input=t, n=3)
print(T)
# tensor([ 3.0000+0.0000j, -1.5000+0.8660j, -1.5000-0.8660j])
# 予め信号をカットした結果と同様になる
print(torch.fft.fft(t[0:3]))
# tensor([ 3.0000+0.0000j, -1.5000+0.8660j, -1.5000-0.8660j])
T = torch.fft.fft(input=t, n=20)
print(T)
# tensor([ 45.0000+0.0000j, -15.4317-31.5688j, -5.0000+15.3884j,
# 2.5741-9.8131j, -5.0000+6.8819j, 4.0000-5.0000j,
# -5.0000+3.6327j, 4.3702-2.5476j, -5.0000+1.6246j,
# 4.4875-0.7919j, -5.0000+0.0000j, 4.4875+0.7919j,
# -5.0000-1.6246j, 4.3702+2.5476j, -5.0000-3.6327j,
# 4.0000+5.0000j, -5.0000-6.8819j, 2.5741+9.8131j,
# -5.0000-15.3884j, -15.4317+31.5688j])
# 予め信号の後ろに0を足した結果と同様になる
t_zero = torch.cat([t, torch.zeros(10)], dim=0)
print(t_zero)
# tensor([0., 1., 2., 3., 4., 5., 6., 7., 8., 9., 0., 0., 0., 0., 0., 0., 0., 0.,
# 0., 0.])
print(torch.fft.fft(t_zero))
# tensor([ 45.0000+0.0000j, -15.4317-31.5688j, -5.0000+15.3884j,
# 2.5741-9.8131j, -5.0000+6.8819j, 4.0000-5.0000j,
# -5.0000+3.6327j, 4.3702-2.5476j, -5.0000+1.6246j,
# 4.4875-0.7919j, -5.0000+0.0000j, 4.4875+0.7919j,
# -5.0000-1.6246j, 4.3702+2.5476j, -5.0000-3.6327j,
# 4.0000+5.0000j, -5.0000-6.8819j, 2.5741+9.8131j,
# -5.0000-15.3884j, -15.4317+31.5688j])信号(正弦波)をFFTして、周波数特性を確認する
PyTorchで正弦波を生成、FFTして周波数特性を確認していきます。
1000Hzの正弦波を作成します。
import matplotlib.pyplot as plt
import numpy as np
A = 0.5 # 振幅
f = 1000.0 # 周波数 Hz
sec = 1.0 # 信号の長さ s
sf = 16000 # サンプリング周波数 Hz
t = torch.arange(0, sec, 1/sf) #サンプリング点の生成
y = A*torch.sin(2*np.pi*f*t) # 正弦波の生成
plt.plot(t, y);
torch.fft.fftを使って、正弦波が1000Hzであることが確認できます。
Y = torch.fft.fft(y)
F = torch.range(0,sf-1,1)
plt.plot(F, torch.abs(Y));
plt.xlim(0,8000)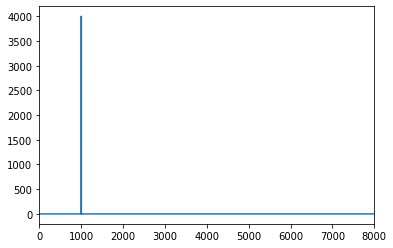

コメント